Coevolving the "Ideal" Trainer
Description of the Problem
One-dimensional Cellular Automata
A one-dimensional cellular automaton (CA) is a linear wrap-around array composed of N cells
in which each cell can take one out of k possible states.
A rule is defined for each cell in order to update its state.
This rule determines the next state of a cell given its current state and the state
of cells in a predefined neighborhood.
For the model discussed in this proposal, this neighborhood is composed of cells whose distance
is at most r from the central cell.
This operation is performed synchronously for all the cells in the CA.
For the work presented in this proposal, the state of cells is binary (k = 2), N = 149 and
r = 3.
This means that the size of the rule space is 2^{2^{2 * r + 1}} = 2^{128}.
Cellular automata have been studied widely as they represent one of the simplest systems in
which complex emergent behaviors can be observed.
This model is very attractive as a means to study complex systems in nature.
Indeed, the evolution of such systems is ruled by simple, locally-interacting components
which result in the emergence of global, coordinated activity.
The Majority Function
The task consists in discovering a rule for the one-dimensional CA
which implements the majority function as accurately as possible.
This is a density classification task, for which one wants the state of the cells of the CA
to relax to all 0's or 1's depending on the density of the initial configuration (IC)
of the CA, within a maximum of M time steps.
Following [Mitchell et al., 1994], $\rho_c$ denotes the threshold for the classification
task (here, $\rho_c = 1/2$), $\rho$ denotes the density of 1's in a configuration and
$\rho_0$ denotes the density of 1's in the initial configuration.
Figure 1 presents two examples of the space-time evolution of a CA
with $\rho_0 < \rho_c$ on the left and $\rho_0 > \rho_c$ on the right.
The initial configuration is at the top of the diagram and the evolution in time of
the different configurations is represented downward.
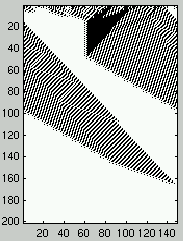
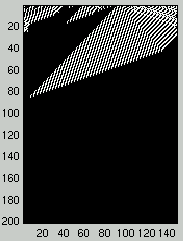
Figure 1: Two space-time diagrams describing the evolution of CA states.
The task $\rho_c = 1/2$ is known to be difficult.
In particular, it has been proven that no rule exists that will result in the CA relaxing
to the correct state for all possible ICs [Land & Belew, 1995].
Indeed, the density is a global property of the initial configuration while individual
cells of the CA have access to local information only.
Discovering a rule that will display the appropriate computation by the CA with the highest
accuracy is a challenge, and the upper limit for this accuracy is still unknown.
Table 1 describes the performance for that task for different
published rules and different values of N along with a new best rule discovered
using the coevolutionary approach presented in this document.
table 1: Performance of different published CA rules and the new best rule
discovered by coevolution for the majority function.
| N |
149 |
599 |
999 |
| Coevolution |
0.863 +/- 0.001 |
0.822 +/- 0.001 |
0.804 +/- 0.001 |
| Das rule |
0.823 +/- 0.001 |
0.778 +/- 0.001 |
0.764 +/- 0.001 |
| ABK rule |
0.824 +/- 0.001 |
0.764 +/- 0.001 |
0.730 +/- 0.001 |
| GKL rule |
0.815 +/- 0.001 |
0.773 +/- 0.001 |
0.759 +/- 0.001 |
The Gacs-Kurdyumov-Levin (GKL) rule was designed in 1978 for a different goal than
the $\rho_c = 1/2$ task [Mitchell et al., 1994].
However, for a while it provided the best known performance.
[Mitchell et al., 1994] and [Das et al., 1994] used Genetic Algorithms (GAs) to explore
the space of rules.
This work resulted in an analysis of some of the complex behaviors exhibited by CAs
using ``particles''.
The GKL and Das rules are human-written while the Andre-Bennett-Koza (ABK) rule has been discovered
using the Genetic Programming paradigm [Andre et al., 1996].
Learning in a Fixed Environment: Evolution
-
Canonical model of evolution
The traditional model for evolutionary approaches to problem solving is to design
a representation for solutions and a fitness function.
The absolute performance of individuals is evaluated with respect to that fitness
function and search operators are used to explore the state space.
As an example, we implemented such an evolutionary approach for the discovery of
CA rules for the $\rho_c = 1/2$ task.
This implementation is similar to the one described in [Mitchell et al., 1994].
Each rule is coded on a binary string of length $2^{2 * r + 1} = 128$.
One-point crossover is used with a 2%$ bit mutation probability.
The population size is n_R = 200 for rules and n_{IC} = 200 for ICs.
The population of ICs is composed of binary strings of length N = 149.
This population is fixed and it is initialized according to a uniform distribution
over $\rho_0 \in [0.0, 1.0]$.
The population of rules is also initialized according to a uniform distribution
over $[0.0, 1.0]$ for the density.
A natural definition for the fitness of rules is the number of Initial Configurations (ICs)
for which the CA relaxes to the correct state:
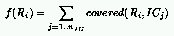
where:

Figure 2 describes the evolution of the distribution of the density of rules over time.
A common behavior resulting from such an evolutionary setup is that
the entire population focuses quickly to a small domain
of the search space in the neighborhood of the current best individual.
Eventually, some progress is observed over time.
The variance for the final performance over several runs is usually large.
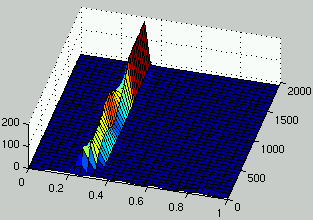
Figure 2: Evolution of the distribution of the density of rules over time.
-
Maintaining diversity by introducing resource sharing
Several techniques have been designed to improve search in a fixed landscape.
Usually those techniques maintain diversity in the population in order to
avoid premature convergence.
[Mahfoud, 1995] presents different niching techniques that are
useful in particular for the exploration of multi-modal landscape.
A technique that we successfully exploited in the past to maintain diversity
is called resource sharing [Juillé & Pollack, 1996].
Resource sharing implements a coverage-based heuristic by
giving a higher payoff to problems that few individuals can solve.
One way to implement this technique for the evolution of CA rules is to define
the fitness of rules as follows:
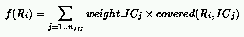
where:

In this definition, the weight of an IC corresponds to the payoff it returns
if a rule covers it.
If few rules cover an IC, this weight will be much larger than if a lot
of rules cover that same IC.
Figure 3 shows the evolution of the distribution of rules density
over several generations.
It can be observed that diversity is maintained for about 500 generations during
which different alternatives are explored simultaneously by the population
of rules.
Then, a solution is discovered that moves the search in the area where density is close
to 0.5.
Afterward, several niches might still be explored, however the coding used to construct
the figures doesn't allow the representation of those different niches since all
the rules have a similar density.
Usually, this technique results in better performance on average.
However, it takes also more time to converge.
This is a trade-off between speed and quality of solutions.
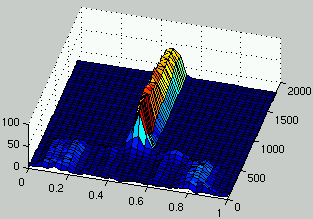
Figure 3: Evolution of the distribution of the density of rules over time.
Learning in an Adapting Environment: Coevolution
The idea of using coevolution in search was introduced by [Hillis, 1992].
In his work, a population of parasites coevolves with a population of sorters.
The goal of parasites is to exploit weaknesses of sorters by discovering input vectors
that sorters cannot solve correctly while sorters evolve strategies to become
perfect sorting networks.
In coevolution, individuals are evaluated with respect to
other individuals instead of a fixed environment (or landscape).
As a result, agents adapt in response to other agents' behavior.
For the work presented in this document, I will define coevolutionary learning
as a learning procedure involving the coevolution of two populations:
a population of learners and a population of problems.
Moreover, the fitness of an individual in a population is defined only
with respect to members of the other population.
Two cases can be considered in such a framework, depending on whether the two populations
benefit from each other or whether they have different interests (i.e., if they are in conflict).
Those two modes of interaction are called cooperative and
competitive respectively.
In the following paragraphs, those modes of interaction are described experimentally
in order to stress the different issues related to coevolutionary learning.
-
Cooperation between populations
In this mode of interaction, improvement on one side results in positive feedback
on the other side.
As a result, there is a reinforcement of the relationship between the two populations.
From a search point of view, this can be seen as an exploitative strategy.
Agents are not encouraged to explore new areas of the search space but only to
perform local search in order to further improve the strength of the relationship.
Following a natural extension of the evolutionary case to the cooperative model,
the fitness of rules and ICs can be defined as follows for the $\rho_c = 1/2$ task:
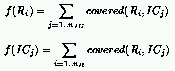
For our experiments, the same setup as the one described previously is used.
The population size is n_R = 200 for rules and n_{IC} = 200 for ICs.
The population of rules and ICs are initialized according to a uniform distribution
over $[0.0, 1.0]$ for the density.
At each generation, the top 95% of each population reproduces to the next generation and
the remaining 5% is the result of crossover between parents from the top 95%
selected using a fitness proportionate rule.
Figure 4 presents the evolution of the density
of rules and ICs for one run using this cooperative model.
Without any surprise, the population of rules and ICs quickly converge to a domain
of the search space where ICs are easy for rules and rules consistently solve ICs.
There is little exploration of the search space.
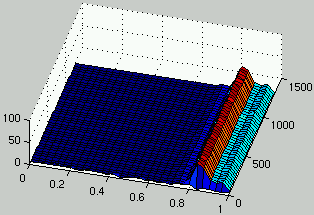
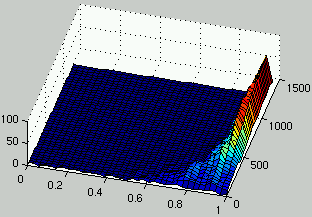
Figure 4:
Evolution of the distribution of the density of rules (left) and the density of ICs (right) over time.
-
Competition between populations
In this mode of interaction, the two populations are in conflict.
Improvement on one side results in negative feedback for the other population.
Two outcomes are possible:
- Unstable behavior: alternatively, agents in one population
outperform members of the other population until those discover
a strategy to defeat the first one and vice versa.
This results in an unstable behavior where species appear
then disappears and reappears again in a later generation.
- a Stable state is reached: this happens if one population
consistently outperforms the other.
For instance, a very strong strategy is discovered by agents
in one population.
For the $\rho_c = 1/2$ task, the fitness defined in the cooperative case
can be modified as follows to implement the competitive model:
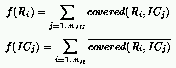
Here, the goal of the population of rules is to discover rules that defeat
ICs in the other population by allowing the CA to relax to the correct state,
while the goal of ICs is to defeat the population of rules by discovering initial
configurations that are difficult to classify.
Figure 5 describes an example of a run using this definition of the fitness.
In a first stage, the two populations exhibit a cyclic behavior.
Rules with low density have an advantage because there are more ICs with low density.
In response to this, ICs with high density have an evolutionary advantage and
have more representatives in the population.
In turn, rules with high density get an evolutionary advantage\ldots
This unstable behavior exhibited by the two populations is an instance
of the Red Queen effect [Cliff & Miller, 1995]: fitness landscapes are changing
dynamically as a result of agents from each population adapting in response
to the evolution of members of the other population.
The performance of individuals is evaluated in a changing environment,
making continuous progress difficult.
A typical consequence is that agents have to learn again what they already knew in the past.
In the context of evolutionary search, this means that domains of the state space
that have already been explored in the past are searched again.
Then, a stable state is reached: in this case, the population of rules adapts
faster than the population of ICs, resulting in a population focusing only
on rules with high density and eliminating all instances of low density rules
(a finite population is considered).
Then, low density ICs exploit those rules and overcome the entire
population.
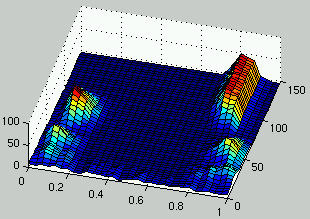
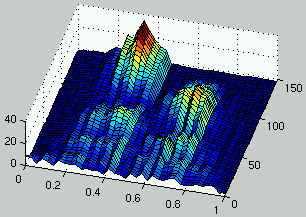
Figure 5:
Evolution of the distribution of the density of rules (left) and the density of ICs (right) over time.
-
Resource sharing and mediocre meta-stable states
We have seen that by introducing resource sharing, it is possible to explore
simultaneously different alternatives by maintaining several niches in the
population.
This section presents some experiments where resource sharing is introduced
in the competitive mode of interaction presented in the previous section.
The fitness of rules and ICs is then defined as follows:
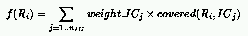
where:

and:
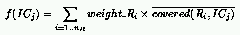
where:
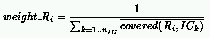
This framework allows the presence of multiple niches in both populations,
each niche corresponding to a particular competence relevant to defeat some
members of the other population.
Figure 6 describes one run for this definition of the interaction between the two populations.
It can be seen that the unstable behavior which was observed in the previous section
doesn't occur anymore and that two species coexist in the population of rules:
a species for low density rules and another one for high density rules.
Those two species drive the evolution of ICs towards the domain of initial configurations
that are most difficult to classify (i.e., $\rho_0 = 1/2$).
However, the two populations have entered a mediocre meta-stable state.
This means that multiple average performance niches coexist in both populations
in a stable manner.
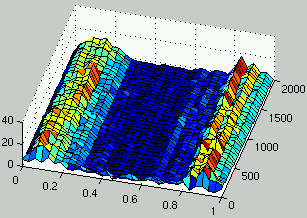
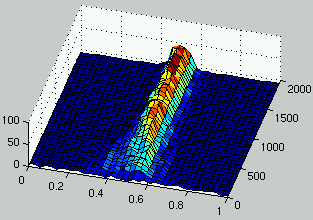
Figure 6:
Evolution of the distribution of the density of rules (left) and the density of ICs (right) over time.
Coevolving the "Ideal" Trainer
The central idea of the coevolutionary learning approach consists in
exposing learners to problems that are just beyond those they know how
to solve.
By maintaining this constant pressure towards slightly more difficult problems,
a arms race among learners is induced such that learners that adapt better
have an evolutionary advantage.
The underlying heuristic implemented by this arms race is that {\em adaptability} is
the driving force for improvement.
In order to achieve this result, our system tries to satisfy the following
two goals:
- to provide an ``optimum'' gradient for search.
This means that the training environment defined by the population of problems
can determine reliably which learners are the most promising at each stage
of the search process.
This means that problems must be informative.
If problems are too difficult or too easy, learners get little feedback and
there is no gradient to determine in which direction the search should
focus.
- to allow continuous progress.
The goal is to avoid the Red Queen effect by providing a training environment
which continues to test learners about problems they solved in the past.
In a sense, the training environment must also play the role of memory.
The difficulty resides in the accurate implementation of those concepts
in a search algorithm.
Experimental Results
It is believed, that ICs become more and more difficult to
classify correctly as their density gets closer to the $\rho_c$ threshold.
Therefore, our idea is to construct a framework that adapts the distribution
of the density for the population of ICs as CA-rules are getting better to solve
the task.
The following definition for the fitness of rules and ICs has been used
to achieve this goal:
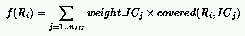
where:

and:
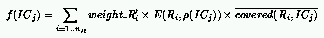
where:

This definition implements the competitive relationship with resource
sharing.
However, a new component, namely $E(R_i, \rho(IC_j))$, has been added
in the definition of the ICs' fitness.
The purpose of this new component is to give a low payoff to IC_j if
ICs with density $\rho(IC_j)$ return little information with respect to
the rule R_i.
We consider that information is collected if rule R_i does better
or worse than random guessing over ICs with density $\rho(IC_j)$
(that is, R_i covers strictly more or strictly less than 50% of those ICs).
Following this idea, we defined E() as the complement of the entropy of
the outcome between a rule and ICs with a given density:
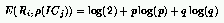
where: p is the probability that an IC with density $\rho(IC_j)$ defeats
the rule R_i and q = 1 - p.
Figures 7 and 8 describe the evolution of the density of rules and ICs for two runs.
It can be seen that, as rules improve, the density of ICs is distributed on
two peaks on each side of $\rho = 1/2$.
In the case of figure 7, it is only after 1,300 generations
that a significant improvement is observed for rules.
It is only at that time that the population of ICs adapts dramatically
in order to propose more challenging initial configurations.
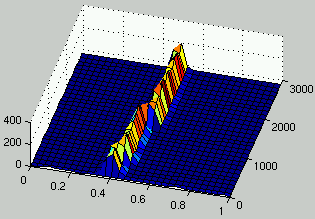
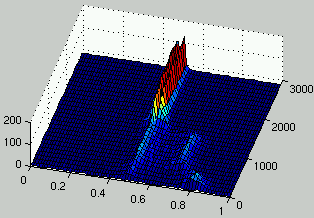
Figure 7:
Evolution of the distribution of the density of rules (left) and the density of ICs (right) over time.
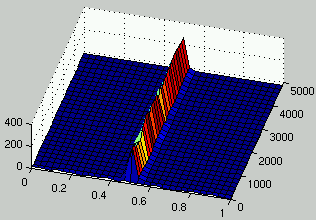
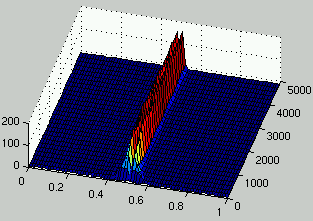
Figure 8:
Evolution of the distribution of the density of rules (left) and the density of ICs (right) over time.
Download our papers about this work:
 Coevolutionary Learning: a Case Study
(with J. B. Pollack),
Proceedings of the Fifteenth International Conference on Machine Learning (ICML-98) ,
Madison, Wisconsin, USA, July 24-26, 1998, to appear.
Coevolutionary Learning: a Case Study
(with J. B. Pollack),
Proceedings of the Fifteenth International Conference on Machine Learning (ICML-98) ,
Madison, Wisconsin, USA, July 24-26, 1998, to appear.
 Coevolving the ``Ideal'' Trainer: Application to the Discovery of Cellular Automata Rules
(with J. B. Pollack),
Proceedings of the Third Annual Genetic Programming Conference (GP-98) ,
Madison, Wisconsin, USA, July 22-25, 1998, to appear.
Coevolving the ``Ideal'' Trainer: Application to the Discovery of Cellular Automata Rules
(with J. B. Pollack),
Proceedings of the Third Annual Genetic Programming Conference (GP-98) ,
Madison, Wisconsin, USA, July 22-25, 1998, to appear.
References
[Andre et al., 1996] Andre, D., Bennet, F. H. & Koza, J. R. (1996). Evolution of intricate long-distance communication
signals in cellular automata using genetic programming. In Artificial Life V: Proceedings of the Fifth International
Workshop on the Synthesis and Simulation of Living Systems. Nara, Japan.
[Cliff & Miller, 1995] Cliff, D. & Miller, G. F. (1995). Tracking the red queen: Measurements of adaptive
progres in co-evolutionary simulations. In the Proceedings of the Third European Conference on Artificial Life,
pp. 200-218. Springer-Verlag. LNCS 929.
[Das et al., 1994] Das, R., Mitchell, M. & Crutchfield, J. P. (1994). A genetic algorithm discovers particle-based
computation in cellular automata. In Parallel Problem Solving from Nature - PPSN III, pp. 344-353.
Springer-Verlag. LNCS 866.
[Hillis, 1992] Hillis, W. D. (1992). Co-evolving parasites improves simulated evolution as an optimization procedure.
In Langton, C. et al. (Eds), Artificial Life II, pp. 313-324. Addison Wesley.
[Juillé & Pollack, 1996] Juillé, H. & Pollack, J.B. (1996).
Co-evolving intertwined spirals. In Proceedings of the Fifth Annual Conference on Evolutionary Programming,
pp. 461-468. MIT Press.
[Land & Belew, 1995] Land, M. & Belew, R. K. (1995). No perfect two-state cellular automata for density
classification exists. Physical Review Letters, 74(25):1548-1550.
[Mahfoud, 1995] Mahfoud, S. W. (1995). Niching methods for genetic algorithms. Technical report,
University of Illinois at Urbana-Champaign. IlliGAL Report No. 95001.
[Mitchell et al., 1994] Mitchell, M., Crutchfield, J.P. & Hraber, P.T. (1994).
Evolving cellular automata to perform computations: Mechanisms and impediments.
Physica D, 75:361-391.




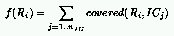


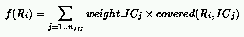


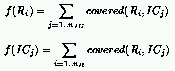


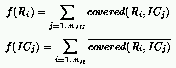


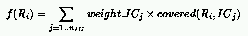

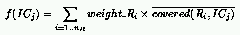
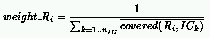


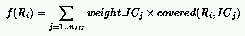

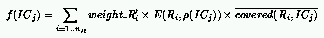

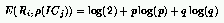




 Coevolutionary Learning: a Case Study
(with J. B. Pollack),
Proceedings of the Fifteenth International Conference on Machine Learning (ICML-98) ,
Madison, Wisconsin, USA, July 24-26, 1998, to appear.
Coevolutionary Learning: a Case Study
(with J. B. Pollack),
Proceedings of the Fifteenth International Conference on Machine Learning (ICML-98) ,
Madison, Wisconsin, USA, July 24-26, 1998, to appear.
 Coevolving the ``Ideal'' Trainer: Application to the Discovery of Cellular Automata Rules
(with J. B. Pollack),
Proceedings of the Third Annual Genetic Programming Conference (GP-98) ,
Madison, Wisconsin, USA, July 22-25, 1998, to appear.
Coevolving the ``Ideal'' Trainer: Application to the Discovery of Cellular Automata Rules
(with J. B. Pollack),
Proceedings of the Third Annual Genetic Programming Conference (GP-98) ,
Madison, Wisconsin, USA, July 22-25, 1998, to appear.